Number Systems ⇒⇒ Exercise 1.4

Question 1

Classify the following numbers as rational or irrational :
(i) 2 - √5
(ii) (3+√23) - √23
(iii)$ { 2√7 \over {7√7}} $
(iv) $ { 1 \over √2} $
(v) 2 $\pi $

Solution :

(i) 2 - √5

Irrational. The difference between a rational number (2) and an irrational number (√5) is always irrational.

Therefore, 2 - √5 is an irrational number.

(ii) (3+√23) - √23 = 3+√23 - √23 = 3

This simplifies to 3, as the irrational parts (√23 and −√23) cancel each other out. It is a rational number as it can be represented in the form of p/q .

Therefore, (3+√23) - √23 is a rational number.

(iii) $ { 2√7 \over {7√7}} $ = $ { 2 \over {7}} $

The √7 in the numerator and denominator cancel each other out, leaving 2/7, which is a ratio of two integers. It is a rational number as it can be represented in the form of p/q.

Thus, $ { 2√7 \over {7√7}} $ is a rational number.

(iv) $ { 1 \over √2} $

Since, this given number is a division of a rational and an irrational number.

Therefore, $ { 1 \over √2} $ is an irrational number.

(v) 2 $\pi $ = 2 × $\pi $

The product of a non-zero rational number (2) and an irrational number (π) is always irrational.

Therefore, 2 $\pi $ is an irrational number.

Question 2 (i)

Simplify each of the following expressions:
(i) (3+√3)(2+√2)

Solution :

(i) We use the distributive property to multiply the binomials.

${ (3 √3) (2 + √2) }$

${ (3 × 2) + (3 ×√ 2) + (√3 × 2) + (√3 × √2) }$

${ 6 + 3√2 + 2√3 + √6 }$

Since the terms have different irrational parts, they cannot be combined further.

Question 2 (ii)

Simplify each of the following expressions:
(ii) (3+√3) (3 - √3)

Solution :

(ii) ${ (3 + √3) (3 - √3) }$

This expression is in the form of (a+b)(a−b),which simplifies to a² - b²

Therefore, we have, a = 3 and b = √3

${3^2 - √3^2 }$

${ 9 - 3 }$

${ = 6 }$

Question 2 (iii)

Simplify each of the following expressions:
(iii) (√5 + √2)²

Solution :

(iii) ${ (√5 + √2)^2 }$

This expression is in the form of (a+b)²,which simplifies to a² + b² +2ab

Therefore, we have, a = √5 and b = √2

${(√5)^2 + (√2)^2 + 2 × √5 × √2}$

${5 + 2 + 2√10 }$

${ = 7 + 2√10}$

Question 2 (iv)

Simplify each of the following expressions:
(iv) (√5 - √2)(√5 + √2)

Solution :

(iv) (√5 - √2)(√5 + √2)

This expression is in the form of (a − b)(a + b),which simplifies to a² - b²

Therefore, we have, a = √5 and b = √2

${(√5)^2 - (√2)^2 }$

${5 - 2 }$

${ = 3}$

Question 3

Recall, $\pi $ is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, $\pi $ = c/ d .This seems to contradict the fact that $\pi $ is irrational. How will you resolve this contradiction?

Solution :

Remember that when you measure a length with a scale or any other instrument, you only obtain an approximate rational value.

You never obtain an exact value.

This is the cause that while measuring the circumference of a circle, i.e.$\pi $ only approximate value is taken.

If we calculate the value of $\pi $ is almost equal to 22/7 or 3.142857....

Hence, There is no contradiction in the statement ,So, you may not realise that either c or d is irrational.

Question 4

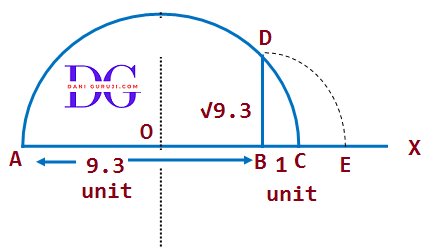
Represent $\sqrt 9.3 $ on the number line.

Solution :

Step 1 – First of all,Draw a horizontal line and mark the distance 9.3 unit from point A on the line so that AB = 9.3 unit.

Step 2 – Then, extend it to point C so that BC = 1 unit.

Step 3 - Now identify the midpoint of line AC. Assume centre point comes at O.

Step 4 - Draw a semicircle taking OC as radius and centre at O.

Step 5 - Draw a line that is perpendicular to AC and passes through B also this perpendicular cut the semicircle at point D.

Step 6 - BD will become equal to $\sqrt 9.3 $

( BD is exactly $\sqrt 9.3 $. This is because in the semicircle construction, the perpendicular from a point on the diameter is the geometric mean of the two segments it divides the diameter into. In this case, BD= $\sqrt {AB × BC} $ = $\sqrt {9.3 × 1} $)

Step 7 - Now, Take B as the centre and BD as radius, draw an arc intersecting the number line at point E.

Step 8 - Now, The line segment BE represents the length of √9.3 unit on the number line.

Question 5 (i)

Rationalize the denominators of the following:
(i) ${ 1 \over {\sqrt 7}} $

Solution :

(i)Given that , ${ 1 \over {\sqrt 7}} $

Multiply and divide the expresssion by denominator that is ${\sqrt 7} $

$${ 1 \over {\sqrt 7}} × { {\sqrt 7} \over {\sqrt 7}} $$

$${ {\sqrt 7} \over 7} $$

Question 5 (ii)

Rationalize the denominators of the following:
(ii) ${ 1 \over {\sqrt 7 - \sqrt 6}} $

Solution :

(ii)Given that , ${ 1 \over {\sqrt 7 - \sqrt 6}} $

Multiply and divide the expresssion by denominator that is ${\sqrt 7 + \sqrt 6} $

$${ 1 \over {\sqrt 7 - \sqrt 6}} × { {\sqrt 7 + \sqrt 6} \over {{\sqrt 7 + \sqrt 6}}} $$

( Using the identity,(a+b)(a–b)= a² - b² )

$$ ⇒ { {\sqrt 7 + \sqrt 6} \over {{(\sqrt 7)^2 - (\sqrt 6)^2}}} $$

$$ ⇒ { {\sqrt 7 + \sqrt 6} \over {7 - 6}} $$

$$ ⇒ { {\sqrt 7 + \sqrt 6} \over {1}} $$

$$ ⇒ {\sqrt 7 + \sqrt 6} $$

Question 5 (iii)

Rationalize the denominators of the following:
(iii) ${ 1 \over {\sqrt 5 + \sqrt 2}} $

Solution :

(iii)Given that , $${ 1 \over {\sqrt 5 + \sqrt 2}}$$

Multiply and divide the expresssion by denominator that is ${\sqrt 5 - \sqrt 2} $

$${ 1 \over {\sqrt 5 + \sqrt 2}} × { {\sqrt 5 - \sqrt 2} \over {{\sqrt 5 - \sqrt 2}}} $$

( Using the identity,(a+b)(a–b)= a² - b² )

$$ ⇒ { {\sqrt 5 - \sqrt 2} \over {{(\sqrt 5)^2 - (\sqrt 2)^2}}} $$

$$ ⇒ { {\sqrt 5 - \sqrt 2} \over {5 - 2}} $$

$$ ⇒ { {\sqrt 5 - \sqrt 2} \over {3}} $$

Question 5 (iv)

Rationalize the denominators of the following:
(iv) ${ 1 \over {\sqrt 7 - 2}} $

Solution :

(iv)Given that , $${ 1 \over {\sqrt 7 - 2}} $$

Multiply and divide the expresssion by denominator that is ${\sqrt 7 + 2} $

$${ 1 \over {\sqrt 7 - 2}} × { {\sqrt 7 + 2} \over {{\sqrt 7 + 2}}} $$

( Using the identity,(a+b)(a–b)= a² - b² )

$$ ⇒ { {\sqrt 7 + 2} \over {{(\sqrt 7)^2 - (2)^2}}} $$

$$ ⇒ { {\sqrt 7 + 2} \over {7 - 4}} $$

$$ ⇒ { {\sqrt 7 + 2} \over {3}} $$